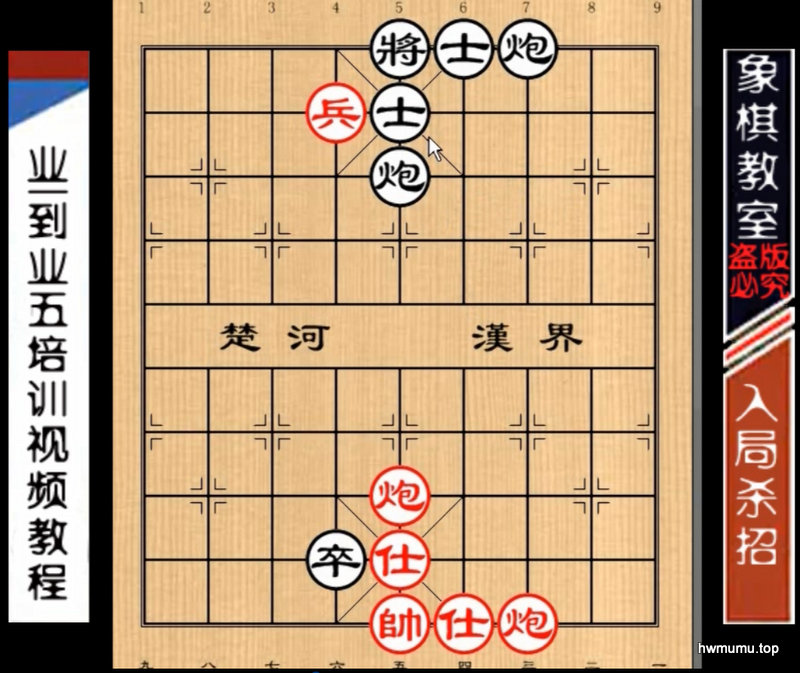
最近在看象棋教室的视频时，发现其介绍了一个残局，说第一步是炮三进八。

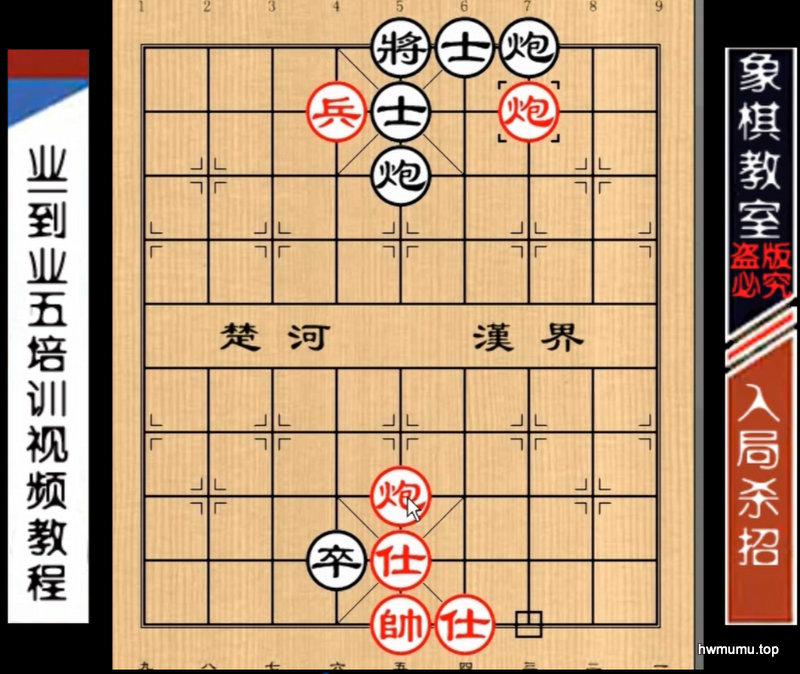
我顿时就产生了疑问，因为如果黑方此时走，炮5进4就赢了，因为此时红三路炮只能退，黑方一路逼，红方炮退到底就输了。

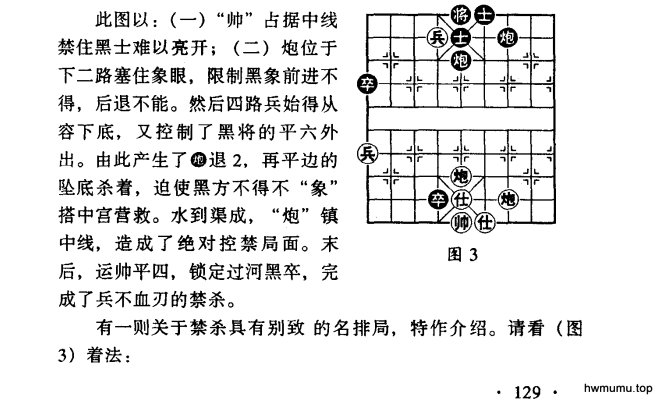
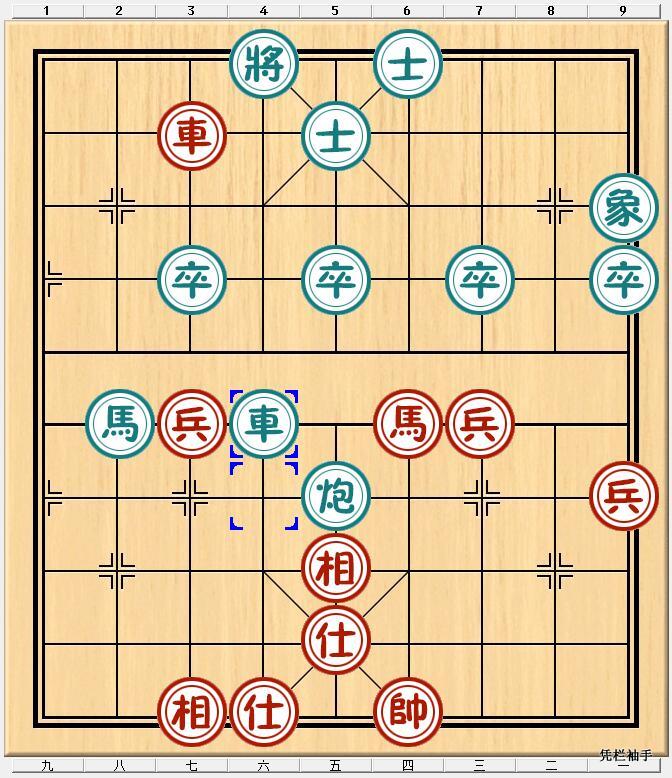
查到贾题韬《象棋残局新论》（成都时代出版社，1991年6月）里面介绍了两个类似的残局，其一是图3，这个局面的原始出处应该是清代古谱《竹香斋象戏谱》中的《双炮禁双炮》局，也叫《盲公顶棍》、《顶顶炮》、《顶顶棍》、《牛顶牛》或《曹操逼宫》等。

其红先胜解法正确，其对参考图的说明也是正确的，红先负。本文旨在说明为什么说这个解法正确。

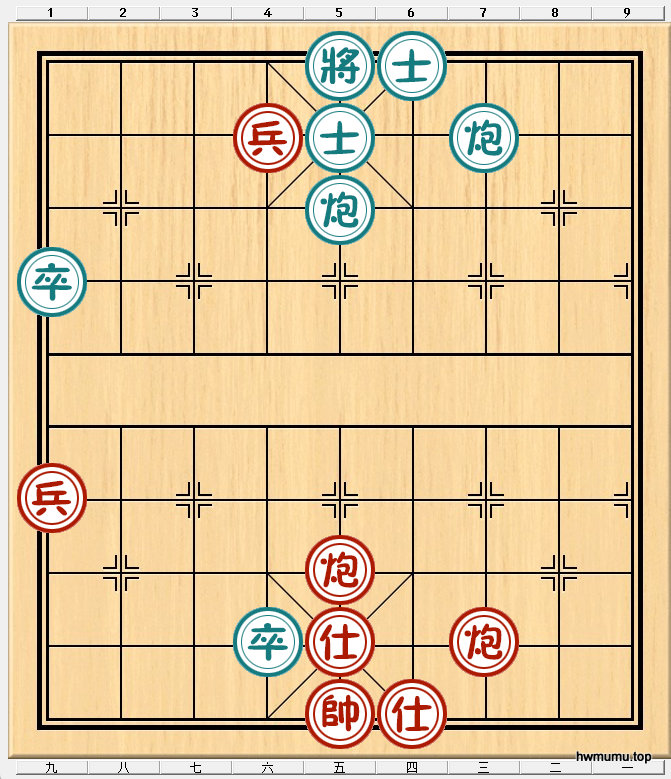
我们定义一个三元数组表达这个局面：B（1，4，6），R代表红方走完（B代表黑方走完，即红先），兵卒之间只能拱一步，否则会被对方吃，因此记为1，五路炮之间有四格，记为4，三7炮之间有六格，记为6 。

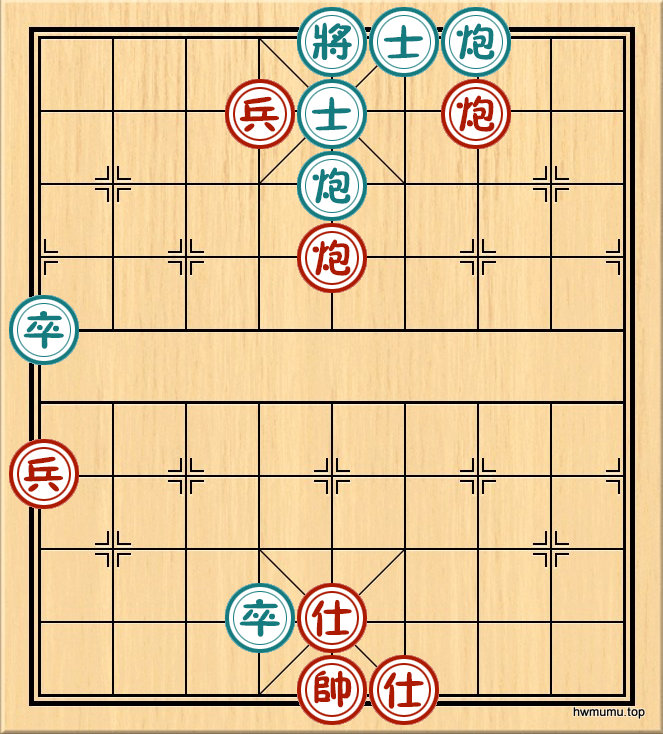
根据贾先生的着法，红方走完第九步炮三进一之后形成如上局面，黑方欠行，必败。根据我们上面的定义，此局面对应的三元数组为：R（0，0，0）。倒推上一步，离此最近的另一个红方赢棋局面为：R（0，1，1），其实可以推广到：R（0，a，a）、R（a，a，0）、R（a，0，a）等均为赢棋局面。

再上一个赢棋局面为：R（1，2，3），若黑方拱卒应B（0，2，3），则红方R（0，2，2）；若黑方走五路炮应B（1，1，3），则红方R（1，1，0）；若黑方动7路炮应B（1，2，2），则红方R（0，2，2）；若黑方7路炮前压两步应B（1，2，1），则红方R（1，0，1），黑方只有这四种应法，均为红胜。

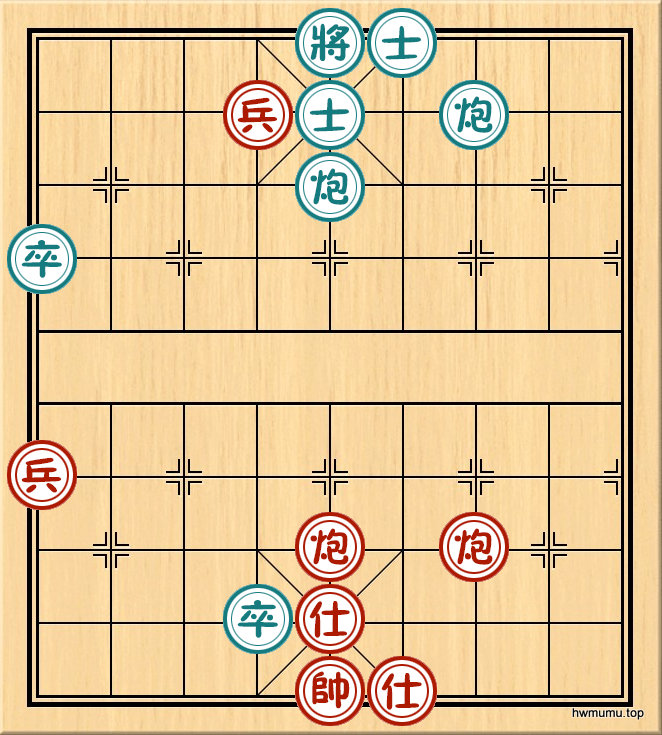
贾先生走完第一步兵三进一之后局面为：R（1，4，5），此时黑方有三种应法：

其一，拱卒，即B（0，4，5），则红方R（0，4，4）；

其二，走中炮，即B（1，a，5），a=0，则红方R（1，0，1）；a=1，则红方R（1，1，0）；a=2，则红方R（1，2，3）；a=3，则红方R（1，3，2）；

其三，走7路炮，即B（1，4，a）,  a=0，则红方R（1，1，0）；a=1，则红方R（1，0，1）；a=2，则红方R（1，3，2）；a=3，则红方R（1，2，3）；a=4，则红方R（0，4，4）；

因此，R（1，4，5）是继R（1，2，3）之后的下一个赢棋局面。通过检查贾先生的着法，易见均为红棋的赢棋局面，因此说贾先生的解法正确。

那么，R（0，0，0）、R（0，1，1）、R（1，2，3）和R（1，4，5）有什么共同点呢？

进一步的讨论

1、我们引入一个概念：异或（exclusive OR，缩写成xor），这是一个数学运算符。它应用于逻辑运算。异或的数学符号为“⊕”，计算机符号为“xor”。其运算法则为：a⊕b = (¬a ∧ b) ∨ (a ∧¬b)

如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。异或也叫半加运算，其运算法则相当于不带进位的二进制加法。

运算法则：
1. a ⊕ a = 0

2. a ⊕ b = b ⊕ a

3. a ⊕b ⊕ c = a ⊕ (b ⊕ c) = (a ⊕ b) ⊕ c;

4. d = a ⊕ b ⊕ c 可以推出 a = d ⊕ b ⊕ c.

5. a ⊕ b ⊕ a = b.

2、我们计算R（0，0，0）、R（0，1，1）、R（1，2，3）和R（1，4，5）的异或值：

0⊕0⊕0=0

0⊕1⊕1=0

1⊕2⊕3=0

1⊕4⊕5=0（我们具体看看这个，4和5的二进制分别为100和101，因此4⊕5=001=1，1⊕1=0）

也就是说红方赢棋局面下的异或值均为0 。

我们看看起始盘面B（1，4，6）的异或值，4⊕6=100⊕110=010，1⊕4⊕6=001⊕010=011，不等于零。

3、也就是说，异或值不为零的起始局红方必胜（取胜方法是使每一步的异或值均为零），否则红方必败。我们来看看贾先生的参考图：

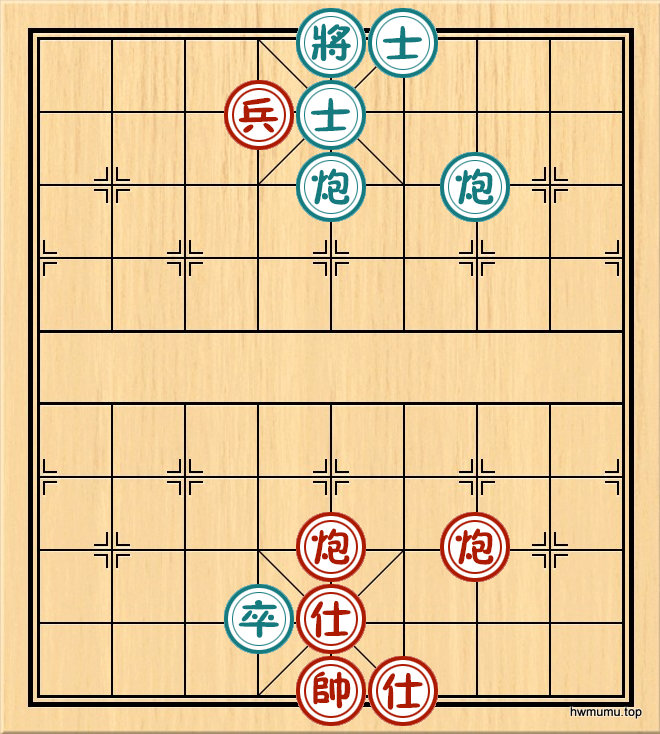
按我们前面定义的局面表达方式为：B（4，4），而4⊕4=0，因此红方必败。

4、本文开篇象棋教室残局的局面为：B（4，8），4⊕8=0100⊕1000=1100 , 不为零，红方必胜，着法是R（4，4）。

5、我们再看一个：

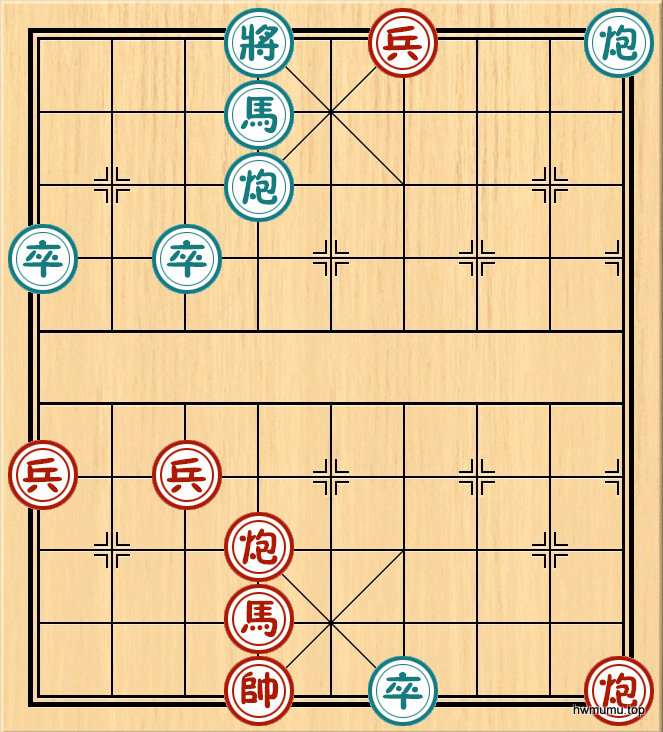
其局面为：B（1，1，4，8），而1⊕1⊕4⊕8=4⊕8=1100，不为零，因此是红先胜。着法是炮一进四，即变成R（1，1，4，4）, 易见1⊕1⊕4⊕4=0 。黑炮横移时，红炮跟着移即可，最多移到三7线，不能回移，否则红炮进底可绝杀。

6、尼姆博弈（Nimm Game，这一名称是由哈佛大学的CharlesL. Bouton命名的，他在1901年提出了此博弈的完整理论）。设有n堆不同的物品，这些堆中各自物品的数量a1、a2、…、an是任意的。两名玩家（R、B）在轮流行动时，可以选择将某一堆中任意数量的物品拿走，至少1个，至多全部拿走，但不能不拿或跨堆拿取物品。根据规则拿到最后一个物品，使得对手无物品可拿的玩家获胜。R先行，起始局势记为：B（a1、a2、…、an）

定义：物品堆的尼姆和（(Nim Sum)）是一个二进制数，它是由所有物品堆中物品的数量转换为二进制后，进行异或运算得到的。物品堆的尼姆和定义为：

Nim Sum（a1、a2、…、an）=a1⊕a2⊕…⊕an

定理1、在尼姆和为0时，无论如何拿取物品，拿取之后物品堆的尼姆和一定不为0；
定理2、在尼姆和不为0时，总存在一种拿取物品的方式，使得拿取之后物品堆的尼姆和为0。

证明：设共有n堆物品，并对第i堆进行了一次拿取操作。在拿取之前各物品堆的数量记为（a1、a2、…、an），其尼姆和记为s，在拿取之后各物品堆的数量记为（b1、b2、…、bn），其尼姆和记为t
根据异或的性质，下面的等式成立：

t=0⊕t=(s⊕s)⊕t=s⊕(s⊕t)=s⊕(a1⊕a2⊕…⊕an)⊕(b1⊕b2⊕…⊕bn)=s⊕(a1⊕b1)⊕(a2⊕b2)⊕…⊕(ai⊕bi)⊕…⊕(an⊕bn)=s⊕0⊕0⊕…⊕(ai⊕bi)⊕…⊕0=s⊕ai⊕bi

1、当s=0，则无论如何拿取物品，都有ai≠bi，即有 t=s⊕ai⊕bi=0⊕ai⊕bi≠0

2、当s≠0，

令 bi=s⊕ai，即有，t=s⊕ai⊕bi=s⊕ai⊕(s⊕ai)=0

证毕。

定理1意味着若物品堆的尼姆和为0，则无论先手方如何拿取，操作之后物品堆的尼姆和一定不为0，先手方总是不能将物品拿完。后手方总是可以选择拿取方式使得物品堆的尼姆和再次为0，同时物品的数量严格减小，这样操作下去，有限多轮之后即可使得后手方拿取物品后所有物品均被拿取，即后手方有必胜策略。

定理2意味着若物品堆的尼姆和不为0，则先手方总可以选择拿取方式使得拿取之后物品堆的尼姆和为0，此时轮到后手方拿取，即先手方有必胜策略。

7、玩家在尼姆博弈中应当按照下面的策略拿取物品：
1.、计算尼姆和s；
2、若s≠0，则计算s与每一个物品堆数量的异或值s⊕ai，直到找到一个s⊕ai＜ai的物品堆，从这一堆中拿取ai-s⊕ai个物品；
3、若s=0，则随意选择拿取物品，此时已经处于必败位置，只能希望对方犯错。

遇到类似《盲公顶棍》的棋局，亦采用此策略。

8、我们注意到《盲公顶棍》和尼姆博弈并非完全等价，后者的数量单调递减，而前者，并非单调递减，有时部分数量还可能增加，因为棋盘上还可以后退。但这点差异不影响第7条的策略运用。

9、尼姆博弈是组合博弈理论(Combinatorial game theory)中的重要模型，是斯普莱格–格隆第定理（Sprague–Grundy theorem） 的基础，此定理指出每一个无偏博弈的的特定局势都可以转换成某种状态的尼姆博弈。利用此定理与构造特定的SG函数(Sprague–Grundy function)，可以解决很多类似的问题。